Konten [Tampil]

Pada materi sebelumnya kita telah menyelesaiakan SPL 3 Variabel dengan masing-masing cara Substitusi eliminasi, Gauss Jordan dan Determinan. Kali ini kita akan Selesaikan Persamaan Linear 3 Variabel dengan ketiga cara diatas. Seperti soal Berikut ini !

Soal SPL 3 Variabel dan penyelesaian cara substitusi, eliminasi, gauss-jordan

Berikut ini Soal SPL 3 Variabel dan Penyelesaiannya menggunakan Cara Eliminasi substitusi, Gauss Jordan dan Determinan.

Contoh soal :

x + y + 2z = 9

2x + 4y -3z = 1

3x + 6y -5z = 0

Cara 1 Penyelesaian SPLTV Metode Substitusi Eliminasi

x + y + 2z = 9 ............................ (1)

2x + 4y + 3z = 1 .......................... (2)

3x + 6y - 5z = 0 ........................... (3)

Dari persamaan (1) dan (2)

x + y + 2z = 9 : (dikali 2) -------> 2x + 2y + 4z = 18

2x + 4y - 3z = 1 : (dikali 1) -------> 2x + 4y -3z = 1 -

-2y + 7z = 17 ........... (4)

Dari persamaan (1) dan (3)

x + y + 2z = 9 : (dikali 3) ------------> 3x + 3y + 3z = 27

3x +6y -5z = 0 : (dikali 1) ------------> 3x + 6y -5z = 0 -

-3y + 11z = 27 ..............(5)

Dari persamaan (4) dan (5)

-2y + 7z = 17 : (dikali 3) ------------> -6y + 21z = 51

-3y + 11z = 27 : (dikali 2) ................> -6y + 22z = 54 -

-z = -3

z = 3

Sekarang kita akan menentukan nilai y dengan mensubstitusikan z = 3 ke persamaan (4)

-2y + 7z = 17 ------------> -2y + 7(3) = 17

-2y + 21 = 17

-2y = 17-21

y = -4/-2

y = 2

x + y+ 2z = 9 ------------> x + 2 + 2(3) = 9

x +2 + 6 = 9

x = 9-8

x = 1

Himpunan penyelesaian yang telah kita dapatkan adalah Hp {1,2,3}

Cara 2 Penyelesaian SPLTV metode Cara Determinan

Selesaikan Persamaan Linear tiga variabel (SPLTV) berikut dengan metode Determinan!

x + y + 2z = 9

2x + 4y -3z = 1

3x + 6y - 5z = 0

Untuk menyelesaikan SPLTV berikut kita ubah bentuk persamaan menjadi bentuk matriks

Langkah 1

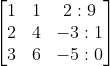
$\begin{bmatrix} 1 & 1 & 2 :9\\ 2 & 4 &-3:1 \\ 3 & 6 &-5:0 \end{bmatrix}$

Langkah 2

Selanjutnya kita akan menentukan nilai Determinan persamaannya sebagai berikut :

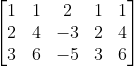
D = $\begin{bmatrix} 1 & 1 & 2 & 1&1\\ 2 & 4 &-3&2&4 \\ 3 & 6 &-5 &3&6 \end{bmatrix}$

D = (1.4.(-5) + 1.(-3).3+2.2.6 )- (2.4.3 + 1.(-3).3+1.2.-5)

D = (-20-9+24)-(24-9-10)

D = -5 - (-4)

D = -5+4

D = -1

langkah 3

Selanjutnya kita akan menentukan Determinan X dengan cara mengganti kolom pertama dengan nilai persamaannya.

Lalu kita perluas matriksnya dengan memindahkan entri pada kolom pertama dan kedua ke sebelahnya. sehingga matriks menjadi berikut ini :

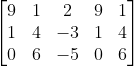
Dx = $\begin{bmatrix} 9 & 1 & 2 & 9&1\\ 1 & 4 &-3&1&4 \\ 0 & 6 &-5 &0&6 \end{bmatrix}$

Kalikan diagonal kanan lalu kurangkan dengan diagonal kiri

Dx= (9.4.(-5) + 1.(-3).0 + 2.1.6) - (2.4.0 + 9.(-3).6+1.1.(-5)

Dx = ( -180 + 0 + 12) - (0 -162-5)

Dx = (-168 - -167)

Dx = -1

Langkah 4

Selanjutnya kita akan menentukan Determinan Y dengan cara mengganti kolom kedua dengan nilai persamaannya.

Lalu kita perluas lagi matriksnya dengan memindahkan entri pada kolom pertama dan kedua ke sebelahnya sehingga matriks menjadi seperti berikut ini :

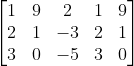
Dy = $\begin{bmatrix} 1 & 9 & 2 & 1&9\\ 2 & 1 &-3&2&1 \\ 3 & 0 &-5 &3&0 \end{bmatrix}$

Kalikan diagonal kanan lalu kurangkan dengan perkalian diagonal kiri

Dy = (1.1.(-5) + 9.(-3).3+2.2.0 ) - (2.1.3+ 1.(-3).0 + 9.2.(-5))

Dy = (-5-81+0)-(6+0-90)

Dy = -86-(-84)

Dy = -2

Langkah 5

Selanjutnya kita akan menentukan Determinan Z dengan cara mengganti kolom ketiga dengan nilai persamaannya.

Lalu kita perluas lagi matriksnya dengan memindahkan entri pada kolom pertama dan kedua ke sebelahnya sehingga matriks menjadi seperti berikut ini :

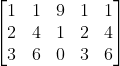
Dz = $\begin{bmatrix} 1 & 1 & 9 & 1&1\\ 2 & 4 &1&2&4 \\ 3 & 6 &0 &3&6 \end{bmatrix}$

Selanjutnya kita operasikan entri entri pada diagonal-diagonal kanan dan dikurangi dengan entri-entri pada diagonal kiri.

Dz = (1.4.0+1.1.3+9.2.6)-(9.4.3+1.1.6+1.2.0)

Dz = (0+3+108)-(108+6+0)

Dz = 111 - 114

Dz = -3

Setelah kita mendapatkan nilai Dx, Dy dan Dz selanjutnya kita akan menentukan nilai x, y dan z dengan cara :

X = Dx/D = -1/-1 = 1

Y = Dy/D = -2 / -1 = 2

Z = Dz/D = -3 / -1 = 3

Sehingga himpunan penyelesaian dari persamaan linear tiga variabel soal

x + y + 2z = 9

2x + 4y -3z = 1

3x + 6y - 5z = 0

diatas adalah {1,2,3}

Demikian Penyelesaian Persamaan Linear Tiga Variabel (SPLTV) metode Determinan. Untuk penyelesaian SPLTV bisa juga dilakukan dengan cara Substitusi eliminasi dan metode Gauss Jordan. Selamat belajar semoga membantu.

Cara 3 Penyelesaian SPLTV dengan metode Gauss Jordan

x + y + 2z = 9

2x + 4y -3z = 1

3x + 6y -5z = 0

Untuk menyelesaikan SPLTV dengan metode Gauss Jordan langkah pertama kita akan mengubah bentuk persamaan linear diatas menjadi bentuk matriks sebagai berikut :

langkah 1

$penyelesaian SPLTV gauss jordan$ $spl 3 variabel$

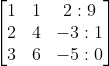
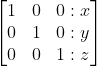
Langkah 2

Kita akan ubah matriks yang ada di sebelah kanan menjadi matriks diagonal yang memuat 1,1,1 pada diagonal utama.

Matriks diagonal /matriks identitas ( I) = $spl 3 variabel$

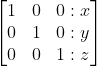
Langkah 3 (kita akan ubah entri pada baris 2 kolom 1 menjadi 0)

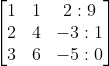
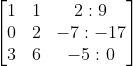$penyelesaian SPLTV gauss jordan$ $\begin{bmatrix} 1 & 1 & 2 : 9\\ 0& 2 & -7:-17\\ 3& 6 & -5:0 \end{bmatrix}$ -2b1 + b2 (-2 dikali baris 1 ditambah baris 2)

Langkah 4 (kita akan mengubah entri pada baris ke-3 kolom 1 menjadi 0)

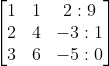
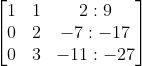$penyelesaian SPLTV gauss jordan$ $\begin{bmatrix} 1 & 1 & 2 : 9\\ 0& 2 & -7:-17\\ 0& 3 & -11:-27 \end{bmatrix}$ -3b1 + b3 (-3 dikali baris 1 ditambah baris 3)

langkah 5 (selanjutnya kita akan mengubah entri pada baris 1 kolom kedua menjadi 0)

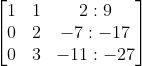$\begin{bmatrix} 1 & 1 & 2 : 9\\ 0& 2 & -7:-17\\ 0& 3 & -11:-27 \end{bmatrix}$ -1/2 b2 + b1 (-1/2 dikali baris 2 ditambah baris 1)

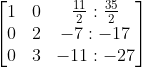
$\begin{bmatrix} 1 & 0 & \frac{11}{2} : \frac{35}{2}\\ 0& 2 & -7:-17\\ 0& 3 & -11:-27 \end{bmatrix}$

Langkah 6 (mengubah baris kedua kolom kedua menjadi 1)

$\begin{bmatrix} 1 & 0 & \frac{11}{2} : \frac{35}{2}\\ 0& 1 & \frac{-7}{2}:\frac{-17}{2}\\ 0& 3 & -11:-27 \end{bmatrix}$ -1/2 b2 (- 1/2 baris 2)

Langkah 7 (mengubah baris 3 kolom 2 menjadi 0)

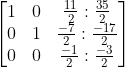$\begin{bmatrix} 1 & 0 & \frac{11}{2} : \frac{35}{2}\\ 0& 1 & \frac{-7}{2}:\frac{-17}{2}\\ 0& 0 & \frac{-1}{2}:\frac{-3}{2} \end{bmatrix}$ -3b2 + b3 (-3 baris 2 ditambah baris 3)

Langkah 8 (mengubah baris 3 kolom 3 menjadi 1)

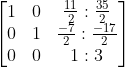
$\begin{bmatrix} 1 & 0 & \frac{11}{2} : \frac{35}{2}\\ 0& 1 & \frac{-7}{2}:\frac{-17}{2}\\ 0& 0 & 1:3 \end{bmatrix}$ -2 b3 (-2 dikali baris 3)

Langkah 9

Sampai di langkah ini kita lihat bahwa diagonal utama sudah menunjukkan 1,1,1 artinya kita boleh memodifikasi langkah dengan cara lain yakni cara substitusi eliminasi.

Jika kita ubah menjadi bentuk persamaan akan menjadi :

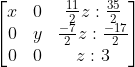
$\begin{bmatrix} x & 0 & \frac{11}{2}z : \frac{35}{2}\\ 0& y & \frac{-7}{2}z:\frac{-17}{2}\\ 0& 0 & z:3 \end{bmatrix}$

Dari matriks diatas dapat kita simpulkan bahwa

z = 3

y + -7/2 z = -17/2 ------------------------> y + (-17/2). 3 = -17/2

y = 2

x + 11/2 z = 35/2 -----------------------> x + 11/2 . 3 = 35/2

x = 35/2 - 33/2

x = 2/2

x = 1

Sehingga dapat disimpulkan bahwa X = 1, Y = 2, Z = 3 atau Hp : {1,2,3

artikel lainnya : Aplikasi SPLTV

Contoh 2

Selesaikan Persamaan Linear Tiga Variabel berikut ini dengan menggunakan cara Determinan, Gauss Jordan dan Substitusi Eliminasi!

2x -3y + 3z = 3

x - y - 2z = -1

-x + 2y - 3z = -4

Penyelesaian Cara Determinan

Langkah 1 : Menentukan Determinan ( D )

D =

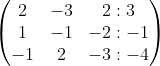
$\begin{pmatrix} 2 & -3 &2 :3 \\ 1& -1&-2 : -1 \\ -1& 2 & -3 : -4 \end{pmatrix}$

D =

$spl 3 var metode determinan$

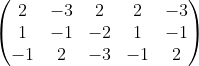
D = ( 2. (-1). (-3) + (-3). (-2). (-1)) - ( 2. (-1). (-1) + 2. (-2). 2 + (-3). 1. (-3))

D = ( 6 - 6 + 4) - ( 2 - 8 + 9 )

D = (4 - 3)

D = 1

Langkah 2 Menentukan Determinan y (Dy)

Tukar kolom pertama dengan nilai persamaannya

Dx =

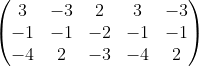
$\begin{pmatrix} 3 & -3 &2 &3&-3 \\ -1& -1&-2 &-1&-1 \\ -4& 2 & -3 &-4&2 \end{pmatrix}$ kolom 1dan 2 di perluas menjadi kolom 4 dan 5

Dx = ( 3.(-1). (-3) + (-3).(-2).(-4)+(2.(-1).2) - ( 2).(-1).(-4) + 3.(-2).2 + (-3).(-1).(-3))

Dx = (9 - 24 - 4 ) - ( 8 - 12 - 9 )

Dx = ( -9 - (-13))

Dx = -6

Langkah 3 Menentukan Determinan y (Dy)

Tukar kolom ke-2 dengan nilai persamaannya

Dy =

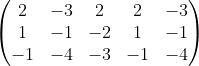
$\begin{pmatrix} 2 & -3 &2 &2&-3 \\ 1& -1&-2 &1&-1 \\ -1& -4 & -3 &-1&-4 \end{pmatrix}$ kolom 1 dan 2 di perluas / ditambahkan ke kolom 4 dan 5

Dy = (2. (-1). (-3) + (-3). (-2). (-1) + ( 2.1. (-4) - ( 2. (-1). (-1) + 2. (-2). (-4) + (-3).1.(-3))

Dy = (6 + 6 - 8 ) - ( 2 + 16 - 9)

Dy = 4 - 9

Dy = -5

Langkah 4 Menentukan Determinan z (Dz)

Tukar kolom ke-3 dengan nilai persamaannya

Dz =

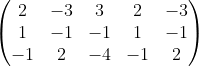
$\begin{pmatrix} 2 & -3 &3 &2&-3 \\ 1& -1&-1 &1&-1 \\ -1& 2 & -4 &-1&2 \end{pmatrix}$ kolom 1 dan 2 di perluas / ditambahkan ke kolom 4 dan 5

Dz = (2. (-1) .(-4) + (-3).(-1).(-1)+ 3.1.(-2)) - (3.(-1).(-1) + 2. (-1).2 + (-3).1.(-4)

Dz = (8 - 3 - 6 ) - ( 3 - 4 + 12)

Dz = 11 - 11

Dz = 0

Dari hasil Determinan masing-masing variabel Dx. Dy, dan Dz kita akan menentukan nilai x, y, dan z dengan cara :

X = Dx/ D = (-6) / 1 = 6

Y = Dy / D = (-5) / 1 = -5

Z = Dz / D = 0 / 1 = 0

Sehingga himpunan penyelesaian untuk persamaaan Linear tiga variabel diatas adalah { -6, -5, 0}

Penyelesaian Cara Eliminasi Gauss Jordan

Selesaikan persamaan linear berikut ini dengan metode eliminasi Gauss Jordan :

2x -3y + 2z = 3

x - y -2 z = -1

-x +2y -3z = -4

Penyelesaian

langkah 1

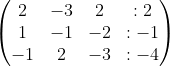
$\begin{pmatrix} 2 & -3 &2 &:2 \\ 1& -1&-2 & :-1 \\ -1& 2 & -3 & :-4 \end{pmatrix}$

langkah 2 perhatikan baris 1

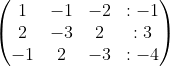$\begin{pmatrix} 1 & -1 &-2 &:-1 \\ 2& -3&2 & :3 \\ -1& 2 & -3 & :-4 \end{pmatrix}$ b1 ---> b2 (baris 1 tukar dengan baris 2)

Langkah 3 : Perhatikan baris 2 dan 3 (akan kita jadikan entri pada kolom 1 baris 2 dan 3 menjadi 0)

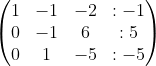$\begin{pmatrix} 1 & -1 &-2 &:-1 \\ 0& -1&6 & :5 \\ 0& 1 & -5 & :-5 \end{pmatrix}$ -2b1+ b2 -----> b2 (-2 baris 1 ditambah baris 2 di baris ke-2)

b1 + b3 ------> b3 (baris 1 tambahkan dengan baris 3 )

langkah 4 : perhatikan baris 3 (akan kita jadikan nilai 1 menjadi 0)

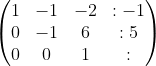$\begin{pmatrix} 1 & -1 &-2 &:-1 \\ 0& -1&6 & :5 \\ 0& 0 & 1 & : \end{pmatrix}$ b2 + b3 ----->b3 ( baris 2 ditambah baris 3)

Langkah 5 : perhatikan baris 2 entri (-1) akan kita jadikan 0)

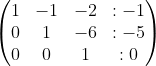$\begin{pmatrix} 1 & -1 &-2 &:-1 \\ 0& 1&-6 & :-5 \\ 0& 0 & 1 & :0 \end{pmatrix}$ - b2 -------> b2 (-1 dikali baris 2 )

langkah 6 : perhatikan baris 1 kolom 2 akan kita jadikan 0

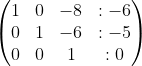$\begin{pmatrix} 1 & 0 &-8 &:-6 \\ 0& 1&-6 & :-5 \\ 0& 0 & 1 & :0 \end{pmatrix}$ b2 + b1 -------> b1 (baris 2 ditambah baris 1)

langkah 7 : Perhatikan diagonal utama sudah menunjukkan matriks diagonal 1,1,1 artinya sudah dapat kita cari nilai x, y dan z

Jika diubah ke persamaan maka akan menjadi

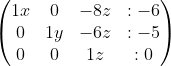
$\begin{pmatrix} 1x & 0 &-8z &:-6 \\ 0& 1y&-6z & :-5 \\ 0& 0 & 1z & :0 \end{pmatrix}$

x -8z = -6 ....................... (4)

y - 6z = -5 ...................... (5)

z = 0

Dari hasil eliminasi kita sudah mendapatkan nilai z = 0, selanjutnya menentukan y dari persamaan (5)

y - 6z = - 5

y - 6 (0) = - 5

y = -5

Nilai x ditentukan dengan mensubstitusi hasil z dan y ke persamaan (4)

x - 8z = -6

x - 8 (0) = -6

x = -6

Sehingga didapat kesimpulan bahwa x, y, z adalah {-6, -5, 0 }

Penyelesaian dengan metode Substitusi Eliminasi

2x -3y + 2z = 3 ........................... (1)

x - y -2 z = -1 ................................ (2)

-x +2y -3z = -4 ............................... (3)

Langkah 1 eliminasi x , ambil persamaan (1) dan (2)

2x -3y + 2z = 3 --- x 1 -----> 2x - 3y + 2z = 3

x - y - 2z = -1 --- x 2 ----> 2x - 2y - 4z = -2 -

- y + 6z = 5 .............. (4)

langkah 2 eliminasi x, ambil persamaan (2) dan (3)

x - y -2 z = -1

-x +2y -3z = -4 +

y - 5 z = -5 ............(5)

langkah 3 eliminasi y, ambil persamaan (4) dan (5)

- y + 6z = 5

y - 5 z = -5 +

z = 0

Substitusikan nilai z = 0 ke persamaan (5) untuk memperoleh nilai y

y - 5z = -5 --------> y - 5(0) = -5 -------> y = -5

Substitusikan nilai z = 0 ke persamaan (2)

x - y - 2z = -1

x - (-5) - 2 (0) = -1

x+5 = -1

x = -1-5

x = -6

Jadi penyelesaian persamaan ini adalah {-6,-5,0}

Demikian penyelesaian Persamaan Linear Tiga Variabel (SPLTV) metode eliminasi Gauss Jordan. Kalian juga bisa melihat cara penyelesaian SPLTV dengan metode determinan dan substitusi eliminasi di blog ini. Serta Aplikasi SPLTV dalam kehidupan sehari-hari

Selamat belajar!

Yurmawita's Blog

Soal SPL 3 Variabel dan Penyelesaian Cara Substitusi Eliminasi, Gauss Jordan dan Determinan

Berikut ini Soal SPL 3 Variabel dan Penyelesaiannya menggunakan Cara Eliminasi substitusi, Gauss Jordan dan Determinan.

Cara 1 Penyelesaian SPLTV Metode Substitusi Eliminasi

Cara 2 Penyelesaian SPLTV metode Cara Determinan

Cara 3 Penyelesaian SPLTV dengan metode Gauss Jordan

Penyelesaian dengan metode Substitusi Eliminasi

No comments

Asus ROG8

About Me

Follow

Popular Posts

Blog Archive

CATEGORY

Pageviews

Affiliated

COMMUNITY

TAGS